En bonne et due forme
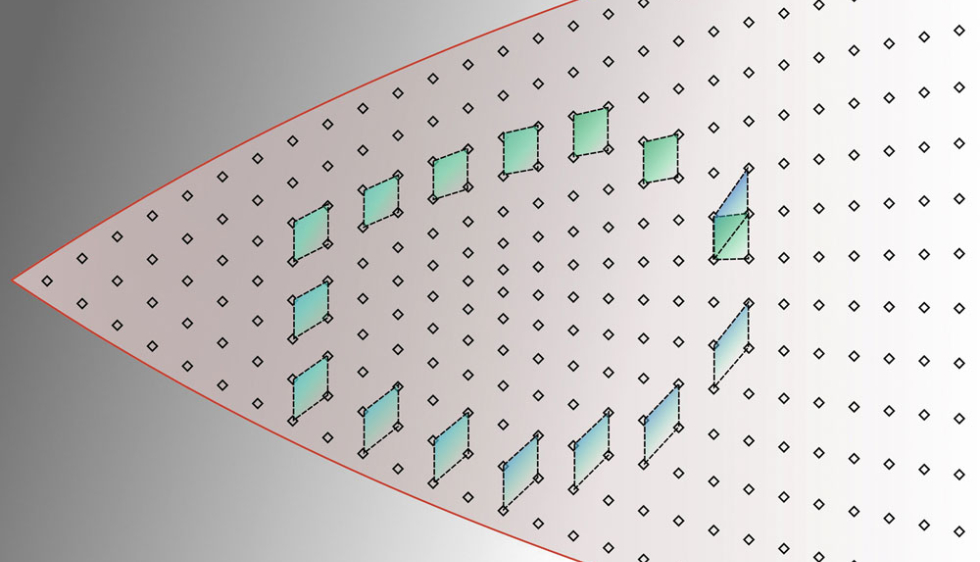
Avec des équations, Yannick Privat cherche des formes optimales répondant à des problèmes de biologie ou de physique.
Quelle est la forme la plus efficace pour laisser s’écouler de l’air. « La première réponse qui vient à l’esprit, c’est un cylindre, un tuyau, souffle Yannick Privat, chercheur à l’ENS Cachan et membre de l’équipe d’analyse de l’Irmar(1). Mais en fait, la forme en question est un peu aplatie, elle correspond à notre trachée, optimisée depuis des siècles grâce à la sélection naturelle. » Et cela se vérifie par le calcul mathématique. C’est l’optimisation de forme, et c’est ce à quoi s’adonne Yannick Privat. « J’essaye de trouver, pour un critère donné, la forme la plus efficace possible. Ce sont des problèmes qui reviennent souvent. Les plus vieux datent de l’Antiquité. Par exemple, trouver la plus grande surface que l’on peut ceindre avec un périmètre donné. Lors de ma thèse, je me suis intéressé à la forme que devait avoir les prothèses pour réparer une artère. Je cherchais à obtenir le meilleur écoulement du sang possible. »
Pour y parvenir, il faut traduire la forme recherchée en une solution – pour l’instant inconnue – d’un problème mathématique. Les critères que l’on cherche à minimiser ou à maximiser (la surface, l’écoulement de fluides... ) s’expriment alors comme des fonctions de cette inconnue. Cela fait intervenir des équations d’un type particulier. « Ce sont des équations dites à dérivées partielles. Les dérivées sont liées aux fonctions par des règles mathématiques bien établies. Elles sont essentielles pour résoudre ces problèmes et obtenir des solutions réalistes. »
Apporter des contraintes
Les critères, quant à eux, sont là pour apporter des contraintes. « En ce moment, nous travaillons sur des formes particulières, dites convexes dans lesquelles il est possible de relier deux points, n’importe lesquels, par un segment, sans sortir. » La plus intuitive des formes qui respecte ce critère, c’est le cercle. Avec une étoile par contre, ça ne fonctionne pas (voir schémas ci-contre). « C’est un thème de recherche important, indique Yannick Privat, car ce critère est un problème omniprésent en mathématiques, qui intéresse aussi bien ceux qui font de l’analyse, comme moi, que ceux qui se penchent sur des problèmes de géométrie. »
 Sur les bords du tambour
Sur les bords du tambour
Une fois les critères choisis, il est possible de faire différentes hypothèses sur les conditions aux bords. « Si l’on veut trouver une membrane qui vibre d’une telle façon, une peau de tambour, par exemple, les équations ne seront pas les mêmes si l’on décide que la peau est bien fixée sur les bords du tambour, auquel cas le déplacement sera nul sur le bord, ou si une partie de la membrane est détachée. » La résolution sera plus ou moins simple suivant les cas.
Prendre le problème à l’envers
En parallèle de ses recherches sur la convexité, le mathématicien a entamé un programme avec des chercheurs du CEA sur la fusion du plasma. Objectif fixé : trouver la forme qu’occupe le plasma dans un réacteur de fusion nucléaire. La difficulté, c’est évidemment que le réacteur est bien fermé, et que les seules mesures possibles se font aux bords. « Les physiciens parviennent à mesurer l’intensité du flux magnétique juste à l’extérieur. Et à partir de ces mesures, nous voulons retrouver la forme qui est à l’intérieur, c’est un problème pris à l’envers ! » Les premiers résultats sont convaincants, et d’ici quelques mois, les chercheurs de ce programme espèrent pouvoir entrer les mesures et faire les calculs en temps réel, un autre défi.
(1) Irmar : Institut de recherche mathématique de Rennes.
Yannick Privat
02 99 05 52 76
Yannick.Privat [at] bretagne.ens-cachan.fr (Yannick[dot]Privat[at]bretagne[dot]ens-cachan[dot]fr)
TOUT LE DOSSIER
du magazine Sciences Ouest